Información del curso
La asignatura de Ecuaciones Diferenciales se organiza en cinco unidades.
En el primer tema se aborda la teoría preliminar para el estudio de los métodos de solución de las ecuaciones diferenciales ordinarias.
En la solución de algunas ecuaciones diferenciales se pueden realizar cambios de variable para reducirlas a separables. Se precisa que en algunos casos un factor integrante puede reducir una ecuación a tipo exacta. Al finalizar esta unidad el estudiante resuelve problemas de aplicación que puedan ser modelados con una ecuación diferencial ordinaria de primer orden.
En el segundo unidad se generalizan las definiciones a ecuaciones diferenciales de orden superior. Se utilizan conceptos del Álgebra Lineal para el estudio de las soluciones de una ecuación diferencial lineal homogénea y se extiende a las soluciones de ecuaciones no homogéneas. Como un ejemplo de ecuaciones con coeficientes variables se presenta la ecuación de Cauchy-Euler considerando los tres diferentes tipos de raíces características.
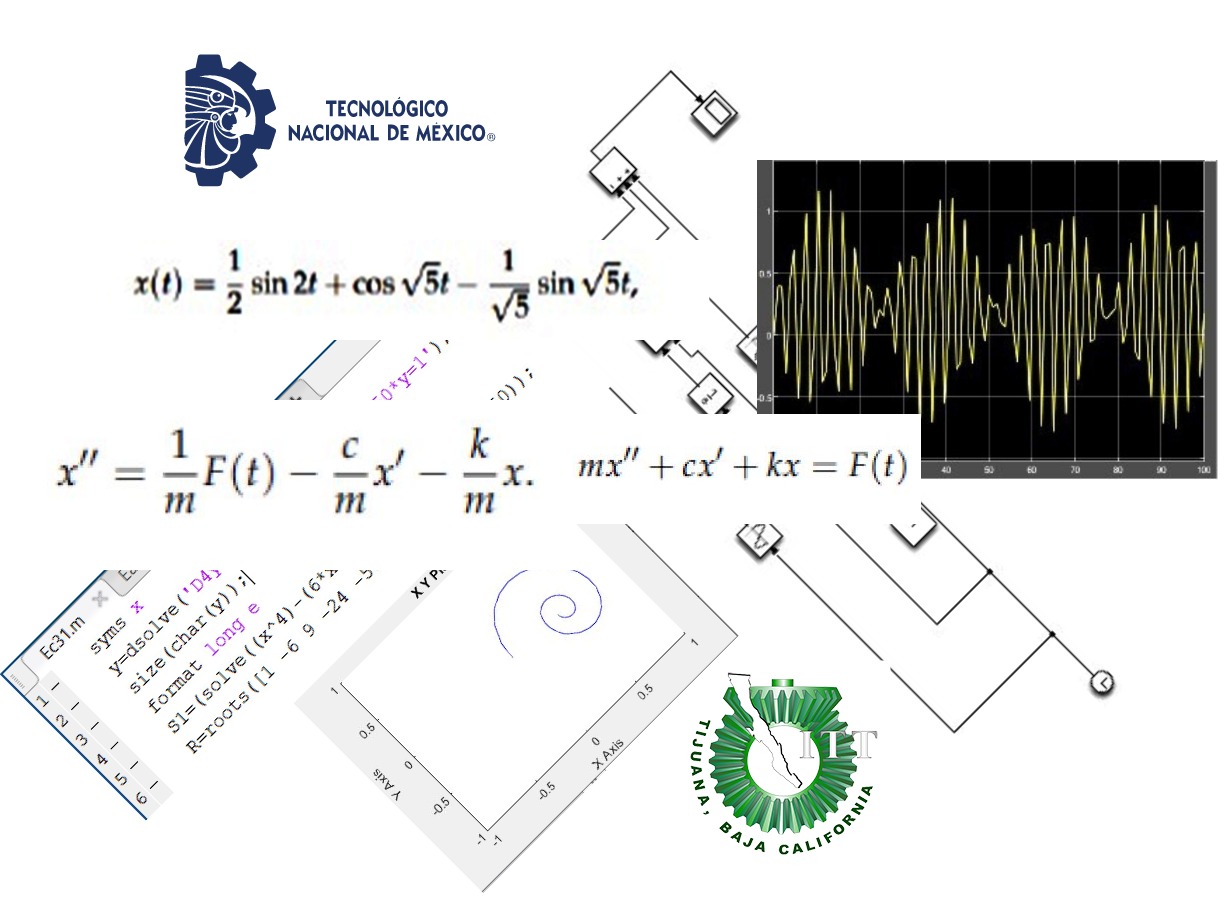
Se modelan y resuelven problemas dinámicos de ingeniería como movimiento vibratorio, circuitos eléctricos en serie, entre otros.
En el tercer unidad se estudia la definición de transformada de Laplace y se discuten sus propiedades de linealidad. Se define la transformada inversa de Laplace como un proceso algebraico inverso. Otros resultados importantes son la derivada de una transformada, la transformada de una derivada y el teorema de convolución que permitirán la solución de un problema de valor inicial utilizando la transformada de Laplace. Finalmente se aborda la función delta de Dirac.
En la unidad cuatro se utilizan los conocimientos adquiridos para modelar y resolver sistemas de ecuaciones diferenciales utilizando operadores y la transformada de Laplace. Se estudian aplicaciones en procesos simultáneos: péndulos, resortes, tanques, brazos robóticos, etc.
La ultima unidad trata de una introducción al estudio de las series de Fourier estableciendo inicialmente los conceptos fundamentales de paridad de funciones y ortogonalidad. Se considera la construcción de series definidas en un intervalo centrado en el origen y definidas en medio intervalo: serie en senos, serie en cosenos y de medio intervalo.
El estudiante debe desarrollar la habilidad para modelar situaciones cotidianas en su entorno.
- Profesor: CARLOS EDGAR VAZQUEZ LOPEZ
